What can you do instead of flash cards to practice multiplication facts with your kids? Multiplication and division fluency is a cornerstone of developing a strong mathematical foundation. The middle and high school students I tutor often struggle with the time and effort it takes to retrieve a calculation fact they were assumed to have memorized in earlier grades. This may not seem like such a big deal…after all, they can just use calculators, right? No, not entirely right. The benefit of spending time exploring and learning multiplication tables is in their ability to foster numerical fluency and flexible mathematical thinking…and these are the true cornerstones of a strong mathematical foundation.
Many of us would like to avoid the flash cards (heck, many of us, including me, have flash card horror stories from childhood), but we don’t know what to replace them with. Flash cards are not bad. If they work for your family, use them. But realize that they are one-dimensional and limited in their power to teach. Really, they are just a way to practice recall. Have you got your facts memorized and can you act under pressure? There is some value to that. But if you haven’t got your facts memorized and/or you freeze under pressure, then what’s the value of the flash cards? They will only serve to give your child one more reason to dislike math. So…try something else. Try activities that build understanding and connections. Activities that foster curiosity and encourage flexible thinking. Activities that strengthen the foundation and framework on which to hang all those math facts. Then…and only then…feel free to whip out the flash cards and see how it goes.
Some related info: automaticity with mulitiplication facts is usually a 3rd grade standard. Before being able to memorize their multiplication facts, students ought to master the concept of what multiplication actually is. There are a variety of ways to visualize or use manipulatives to understand multiplication. For the purposes of this post, I’m going to assume (love that word) that your child’s teacher is handling that part just fine. (Then I’ll write another post where I assume that your child’s teacher is NOT handling that part just fine!) The purpose of THIS post is to answer my friend’s question, “Are flash cards the only way to help my child learn his multiplication facts?”
The answer, of course, is “Nope, they aren’t.” Here is one other way to do it that I particularly like. (And if you have more ideas, please comment and help a parent out!)
- Print out a 20×20 multiplication table (actually, make a handful of copies.) Hand it to your kid when he’s bored or waiting for dinner at a restaurant. Give him some cool highlighters, too. I don’t suggest telling him that this is multiplication practice. (Because in reality it’s not. It’s much more than that. Don’t limit his expectations!) Tell him it’s a kind of puzzle. Ask him what he NOTICES about the table and what he WONDERS about the table. Listen to his answers.
- Or/And tell her the challenge is to find as many patterns in the table as she can. Let her highlight what she sees. Your kid may go to town on this and find all sorts of stuff. Your answer to each observation she makes is to say, “Wow. Nice observation. Tell me more about that. Explain that to me. Does that pattern always continue? Are there more patterns?” On the other hand, your kid may not go to town on this. If she’s open to it, make some suggestions. Start with the skip-counting patterns that match vertically and horizontally (for example: 3rd row is 3,6,9,etc. and 3rd column is 3,6,9,etc.) Skip-counting is just another way to say “count by 3’s” or “count by 2’s.” Along the way, maybe square numbers will stand out. Maybe that pattern that each square number increases by the next odd number will stand out. (These are just examples…you don’t have to know what all the patterns are. Trust your kid to explore and find things you would never have thought of.) The important thing is to interact with the table and get exposure. The process of interacting will built connections in your child’s mind that will help with understanding and recall.
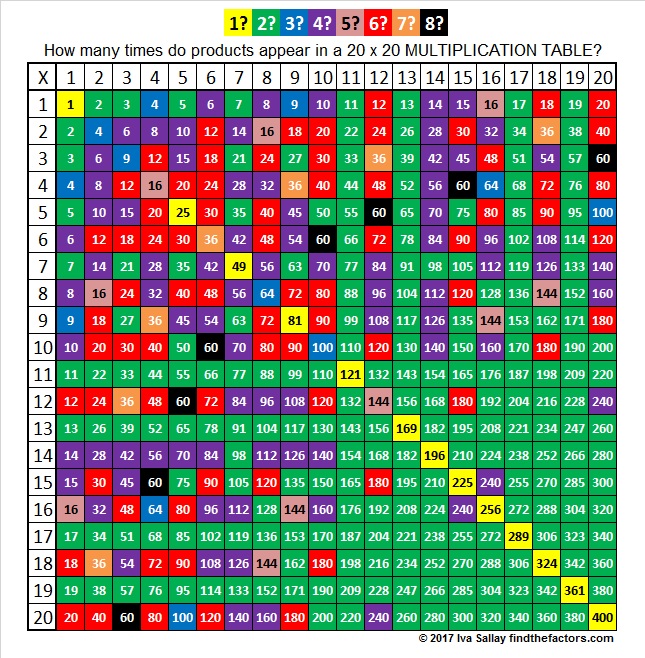
- What if your kid is not interested in going to town with this? Okay. Use it another way. Let your child quiz you on YOUR multiplication recall. Let him hold the table and ask you what 6 x 7 is (that one always takes me a few extra seconds.) Make a mistake now and then (you don’t have to let anyone know whether it was purposeful or not) so that he gets to correct you and build some more connections in his brain. As above, this is a nice thing to bring to a dinner out or some other activity where there will be waiting and you will be happy to have something to pull out of your bag of tricks.
- At some point, leave a blank 20 x 20 multiplication table lying around. Challenge your child to fill in as many as she can. Make sure that you aren’t emotionally attached to whether she can complete the table or not. Then maybe she won’t be either. Because that’s not important. When she gets stuck or slows down, you can help her use patterns to fill out the rest, OR be finished with it. Do it again another time after playing some more with the filled-in table.
- After some time, the patterns and connections will start to stick in your child’s mind. He will feel more confident in his multiplication fact answers because he can not only connect them to the visuals and manipulatives that we hope his teachers are using to explain multiplication, but he can also connect his answer to the patterns and observations he has made with the 20 x 20 table.
(Mathematically…automaticity (memorizing) with math facts is important. Yes, with our ubiquitous phones, many of us have a calculator always at our fingertips. BUT there is good reason to develop automaticity. At the very least, it saves time. I can retrieve the answer to 6 x 7 faster than you can type it into your calculator. And, even in the most wonderful math classrooms in the world, time is short. The faster you can retrieve that math fact, the more time you can spend exploring the deeper patterns of math. MORE important however…the process of building automaticity from a strong foundation of curiosity and understanding helps to build the network of connections that lead to mental flexibility and numerical fluency.)


Leave a comment